Thomas W. Knowles and Associates

OPTIMIZATION SPECIALISTS

Home

Optimization

OPTIMIZATION

An Optimization model chooses the value of decision variables that give the optimal solution. Optimization models have three parts. The first part is a function of the decision variables, called the objective function, that is to be maximized or minimized. Often, the objective is to either maximize profits or minimize costs, but many other objectives are possible depending on the decision environment.

The second part is a set of constraints that limit the combinations of decision variables that can be considered. A constraint function consists of three parts: a constraint function (dependent upon the decision variables), a relationship, and a right-hand-side (RHS). The relationship can be one of <=, >=, and =. An example would be that the number of people working during a time period must be >= some specified value. Or the number of hours used on a machine must be <= the number of hours available.

Decision variable limitations are the third part of an optimization model. These limitations are different from constraints. The most common of these limitations include: (1) the values must not be negative, (2) the values are restricted to integers (General Integer variables), and (3) the values are restricted to 0 or 1 (Binary Integer variables). An example of the first type of limitation would be that the number of pounds of a raw material used couldn’t be negative. An example of the second type of limitation is that the number of people hired must be an integer. The third type of limitation is often used to choose between two discrete alternatives, such as 1 if a distribution center is built and 0 if it is not.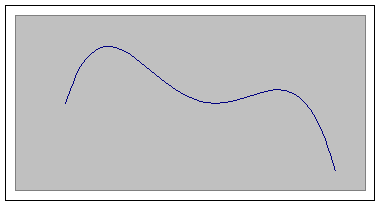

The mathematical form of the model affects what software (and associated algorithm) can be used. If all of the functions---objective and constraints---are linear and the variables are continuous, then it is called a linear programming model. If all of the functions are linear but at least one of the decision variables is either a General Integer or a Binary Integer, the model is called an integer linear programming model. If any of the functions is not linear and all the variables are continuous, then the model is called a nonlinear programming model. An integer nonlinear programming model contains at least one nonlinear function and at least one variable with integer restrictions.

A crucial issue is whether any of the functions---objective or constraint--- is not linear. A nonlinear function can result in the software achieving a “local” optimal solution that is not a “global” optimal solution. The maximum on the right is a local maximum, i.e., it is larger than the values close to it. However, the maximum on the left is also a local maximum, but it is also the global maximum, i.e., the maximum over all decision variable values. Optimization software for nonlinear programming models finds a local optimal solution. Unfortunately, it cannot guarantee that the local optimal solution it finds is also the global optimal solution.

A new global solver option from Lindo Systems, Inc guarantees an optimal solution. However, this extra cost option is frequently not necessary because of the experience we have in linearizing functions that are intrinsically nonlinear.